The fifth assignment consist on, as stated in the pdf:
"Implement a HTTP public-key repository for key exchange that employs RSA-based digital signatures"
To do this I chose python and CGI to implement the web service, because it's pretty simple to link the html form to a python script and then take the data from the form to do all the work. I also used a small javascript function to generate random numbers from 1 to 100, because this was somewhat useful to generate the challenge number x.
Methodology:
First, for a better understanding of the situation, consider this example:
"Alice is chatting with Bob, but she thinks he may be an impostor. Bob is registered in a authentication web service, so Alice enters the web page and generates a challenge "x". Alice then sends this Challenge to bob, who will then Download a script from the web service, in order to calculate his Response "r", which should be generated using a function f(x)[which both the web service and this script should know], the Challenge and his private key. Bob will send Alice back "r", and Alice will then write r in the web service, and selecting Bob in a list. The web service will look for Bob's public key (e, n), and it will calculate its own f(x) which will then compare with r^e % n,. If the values were the same, the web service informs Alice that the authentication was successful. But if the authentication fails the web service will warn Alice that Bob is a fake."
Now I will explain how all fits together step by step in my code:
- Using the previous assignment programs, I generated some public and private keys. And stored the public keys somewhere where the server can find them.
- Alice generates a random challenge value "x" using the web service, and selects Bob from the list. Then Alice will send "x" to Bob using a chat.
- To get the response, Bob will download a script(the link will be in the same page as the form) and will calculate his y = f(x), and then the response r = y^d % n with his private key. Then Bob will send back the response "r" in the chat.
- Alice will type "r" in the form and then when "Check" is pressed, the python script will read all the values, search for the public key of Bob, and calculate r^e % n.
- If the calculated value is equal to f(x) [the server should also know what f(x) is], then Bob is authenticated, otherwise he's not Bob and a warning is issued.
Python Code:
Script for Getting the Response
def f(x):
y = x+1
return y
def exp(x,n):
power = 1
while n != 0:
if n %2 != 0:
power *= x
n -= 1
x *= x
n /= 2
return power
if __name__ == "__main__":
x = int(raw_input("Challenge(x):"))
d = int(raw_input("d:"))
n = int(raw_input("n:"))
y = f(x)
r = exp(y, d) % n
print "Your r = %s"%r
The purpose of this script is for the user to download it and calculate its response "r". To do this the user should know his/her private key (d, n) and the challenge value "x". Giving this data as input, the program will calculate y = f(x), where this function is the same that the web service uses. The script will then calculate:
r = (y^d) % n. This r will be sent back to the person using the web service so it can be written in the form.
Python main code
#!/usr/bin/python
import cgi
def read_public_key(user):
f = open("users.dat", "r")
for line in f.readlines():
tmp_user, public_key = line.split(" ")
if tmp_user == user:
e, n = public_key.split(",")
e = e.replace("(", "")
n = n.replace(")", "")
return (int(e), int(n))
return -1
def f(x):
y = x + 1
return y
def exp(x,n):
power = 1
while n != 0:
if n %2 != 0:
power *= x
n -= 1
x *= x
n /= 2
return power
if __name__ == "__main__":
url = "http://synnick.byethost31.com/"
print "Content-type: text/html\n"
print "<html><head>"
print ' <meta http-equiv="refresh" content="5;url=%s" />'%url
print "<title>Redirecting...</title></head><body><center>"
form = cgi.FieldStorage()
x = int(form.getvalue("Challenge", "(No x value)"))
user = form.getvalue("User", "(No user)")
r = int(form.getvalue("y", "(No response)"))
(e, n) = read_public_key(user)
y = exp(r, e) % n
if y == f(x):
print "<h1>:)</h1>"
print "<h2>User %s is real</h2>"%user
else:
print "<h1>:(</h1>"
print "<h1>User %s is a fake!</h1>"%(user)
print '<form method="link" action="http://synnick.byethost31.com/">'
print '<input type="submit" value="Go Back"></form>'
print "</center></body></html>"
The code is pretty simple. I copied some functions that I used in the previous assignment, like the exp(x, n) function to do exponentiation by squaring, which is faster than the python's default methods. I also copied my function to read the public key of a certain user from a file, but edited it a little bit.
The important part(the cgi handling) is just checking if a certain name of a form field exists, and reading its value if its not empty. This is done for the challenge value, the list with the users and the response. This data will be used by the program, first with the user name the program will read his/her public key from the users.dat file located somewhere in the server. Then with that public key, the web service will calculate y from the response and compare with the value of f(x). Should this be equal, the user is authenticated, and the program shows a happy smiley. If not then the user is not who he/she says and the program shows a sad smiley.This output is easily done printing html code.
Test to the keys:
Using the test routine that was posted in the Facebook group, I ran some tests to keys with different length, the results were:
Using a short key:
(Here the test passed, because both assertions were True)
Using a medium-sized key:
(Here the test also passed)
Using a long key:
(Here using a long key the test didn't passed)
Using a long key with the Facebook Group code:
(The test passed, which means my key generation program doesn't work with large keys)
Example Run:
First, I'll show the files with the private and public keys that I generated:
(The first file is the one I used to save all the generated keys, both public and private so I could use them while running test. The second one is the file that the web service uses to find the public key of a certain user)
Now using Lucy as an example, I generated a random value x, selected Lucy from the list, and "sent the x value to Lucy".
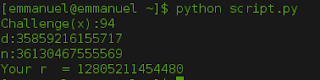
So the generated x was 76, now "Lucy should download the script from the provided link and use it to calculate the response r":
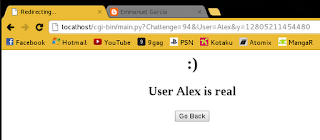
The calculated response value was 115, "Lucy should send this value back to me, so I can type it in the Response field". Now when I press Check, the program should compare the values and show an output depending on the results. In this case:
Now lets imagine that the response that Lucy sent back wasn't 115 but another number like 77. When I click check with this value, the web service will find a mismatch and then this will happen:
Testing Web Service with Long Keys
Using the large keys that I generated using the Facebook group code, the web service worked correctly:
So the problem with my long key generation was with my
exponentiation function, which wasn't fast and good enough than the class
fastmodexp function.
References: